How RSA works?

Before diving into the RSA library, I would like to talk about how RSA works theoretically.

If you would like to RSA encryption, you should generate and publish a public key depending on two large prime numbers, along with a helper value. You have to keep secret your prime numbers. Anyone can send encrypted messages, via the public key, but can only be decoded by someone who knows the private keys which consist on prime numbers.

With RSA, you have to pick two distinct prime numbers (P and Q) at random, and then compute:

N=PQ

And then select e and d (d is the modular multiplicative inverse of e). Your public key is:

Pub=(e,N)

and your private key:

Priv=(d,N)

If you have a message of M, then the encrypted content is:

Enc=M^e (mod N)

and you can decrypt with:

Dec=Enc^d (modN)

Now you have basic concepts of RSA

public-private key cryptosystem, we can move forward more Rust codes.

RSA Encryption in Rust

Our lovely friend Bob has his own key pairs. Alice wants to send a private message to Bob. Thanks to RSA system, she can send a encrypted message using Bob's public key pair.

<RSAKeyValue>
    <Modulus></Modulus>
    <Exponent></Exponent>
</RSAKeyValue>

Above components are his public key components which are given as a string. <Modulus> represents the “N” value, <Exponent> represents the “e” value.

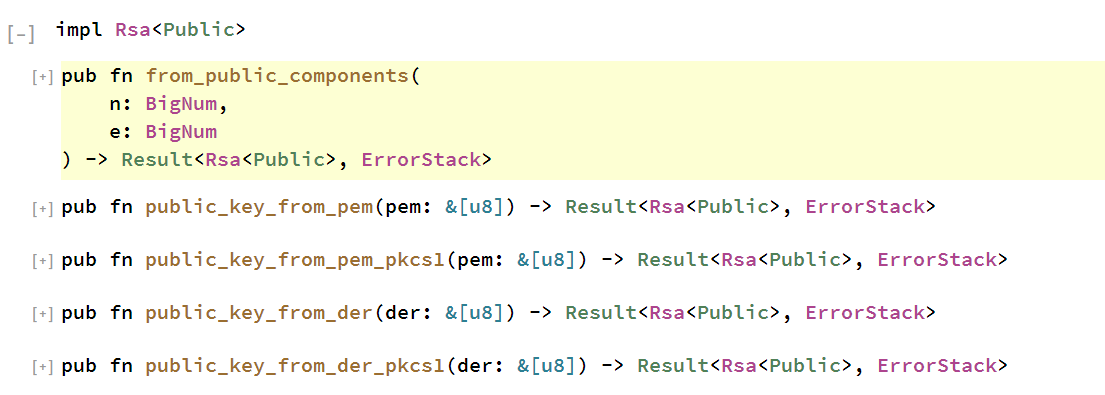
As you can see the image, RSA key struct implements 5 different methods. Since we have all public components, I would use first method to generate public key. Before creating a RSA public key, we have to convert string components into BigNum format.

let n = "your_n_value_as_string";
let decoded_n = BASE64.decode(n.as_bytes()).unwrap();

let e = "your_e_value_as_string";
let decoded_e = BASE64.decode(e.as_bytes()).unwrap();

let big_e=  BigNum::from_slice(&decoded_e )?;
let big_n=  BigNum::from_slice(&decoded_n)?;

Now we have “N” and exponent "e" as BigNum format. Finally, we can create our public key.  I would use below method to encrypt message using the public key, it returns the number of encrypted bytes.

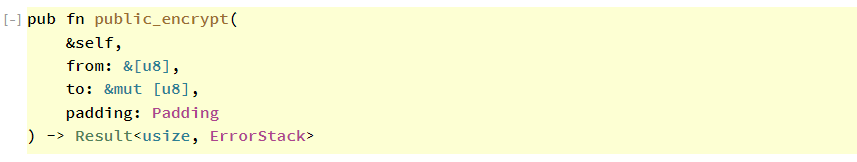
To sign our message using the public key I used public_encrypt method from RSA struct. Public encryption method accepts 3 arguments. First one is data to be encrypted. Public encryption method takes your message as bytes. Second is a buffer to collect returning encrypted bytes. Your buffer size should be same as the RSA key. Lastly you have to specify padding type to use. Padding is used to prevent attackers from estimating or knowing the precise length of a plaintext data that can cause to breaking encryption.

let rsa = Rsa::from_public_components(big_n,big_e).unwrap();

// Encrypt with public key
let mut buf: Vec<u8> = vec![0; rsa.size() as usize];
let _enc = rsa.public_encrypt(message.as_bytes(), &mut buf, Padding::PKCS1_OAEP).unwrap();

//decode the buffer
let b64_encoded_mes = BASE64.encode(buf.as_ref());
println!("Encrypted: {:?}", b64_encoded_mes);

If you would like to take your encrypted data as string, you should encode your message. Now you have encrypted data which can only be decrypted by the corresponding private key!

RSA Decryption in Rust

Now we are ready to decrypt message sent from Alice. As I said before Bob should keep secret his private key. So that nobody can decrypt Bob's messages

<RSAKeyValue>
    <Modulus></Modulus>
    <Exponent></Exponent>
    <P></P>
    <Q></Q>
    <DP></DP>
    <DQ></DQ>
    <InverseQ></InverseQ>
    <D></D>
</RSAKeyValue>

Above components are his private key components which are given as a string. <Modulus> represents the “N” value, <Exponent> represents the “e” value. And I would like to give more detailed information about other parameters. You do not have to worry about what they mean in depth. You just need to post these parameters to the appropriate places.

• d: reference to the private exponent of the key.
• p: reference to the private exponent of the key.
• q: reference to the second factor of the exponent of the key.
• dmp1: reference to the first exponent used for CRT calculations.
• dmq1: reference to the second exponent used for CRT calculations.
• Iqmp: reference to the coefficient used for CRT calculations.

As you can see from the image, RSA Private key struct implements different methods. Since I have all public/private key components I would use first method to generate private key struct. Again, we need to convert all components into BigNum format.

let rsa = Rsa::from_private_components(big_n,big_e,big_d,big_p,big_q,big_dmp1,big_dmq1,big_iqmp).unwrap();

// Decrypt with private key
let mut buf: Vec<u8> = vec![0; rsa.size() as usize];
let _b64_encoded_sig = BASE64.decode(enc_data.as_ref()).unwrap();
let _enc = rsa.private_decrypt(&_b64_encoded_sig, &mut buf, Padding::PKCS1_OAEP).unwrap();
let _b64_encoded_sig = BASE64.encode(buf.as_ref());
println!("Decrypted: {}", String::from_utf8(buf).unwrap()); 

Private decryption method decrypts data using the private key. It takes 3 parameters. First one is encrypted data which is decoded with base64. Second one is our buffer to cumulate decrypted bytes. Last one is padding type which is used in encryption process.

End of the story! You are ready to encrypt/decrypt your messages using Rust OpenSSL library!